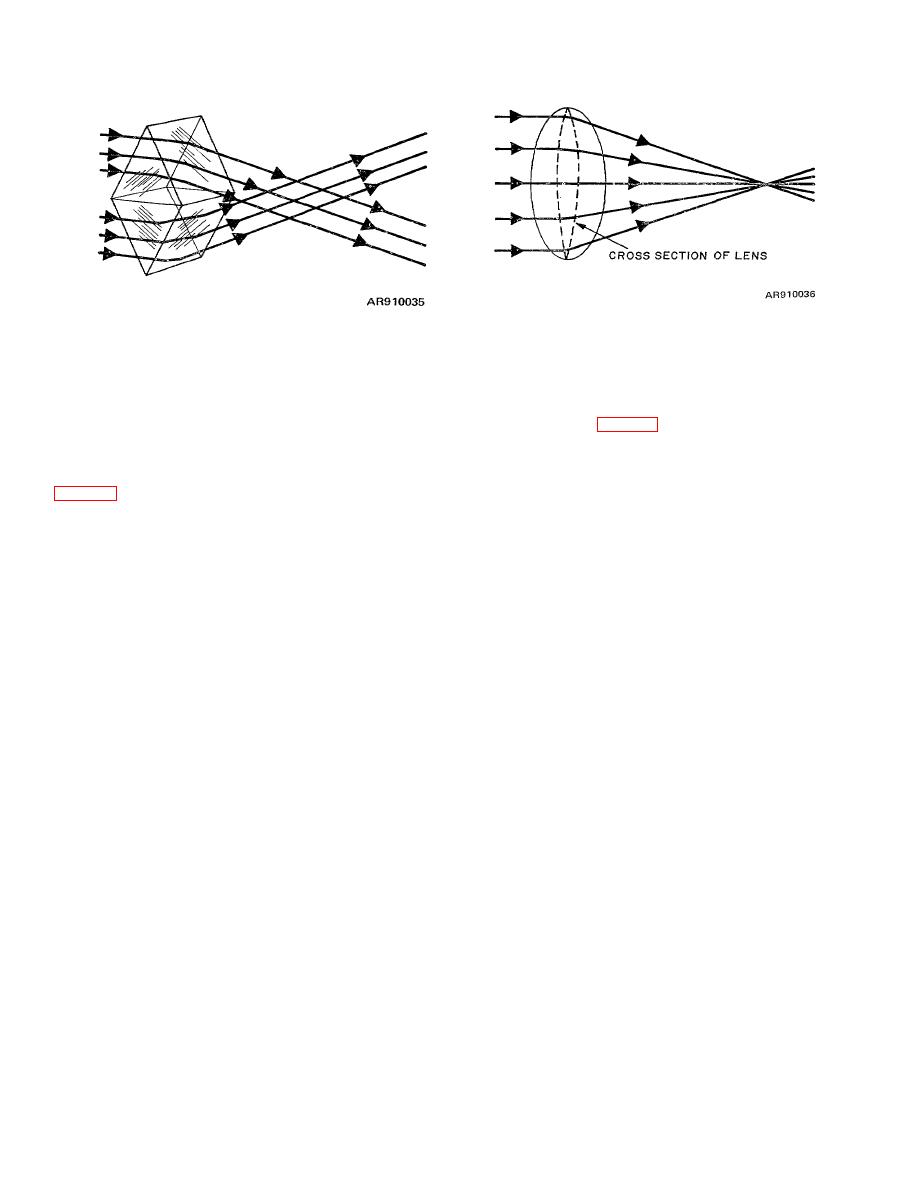
Figure 2-29. Deviation of rays by two prisms, base to base

TM 9-258

Figure 2-29. Deviation of rays by two prisms, base to

Figure 2-30. Deviation of rays by convergent lens

base.

(2) Myriads of rays may be considered to come from

every point of light on an object. Consider the refraction

(1) If the two prisms are cut in semicircular form,

of three such rays from a point of light passing through a

their surfaces made spherical, and the two bases

convergent lens (fig 2-31) to intersect at a point on the

cemented together, the result will be an optical element

other side of the lens. On the basis that a lens bends the

known as a convergent lens. (All convergent lenses are

rays as a prism does, rays passing through the upper

thicker at the center than at the edges. ) When parallel

and lower portions of the lens would be bent toward the

rays of light strike the front surface of a convergent lens

thickest part of the lens upon striking the first surface

(fig 2-30), all rays pass through the lens and converge to

and bent again toward the thickest part in emerging. As

a single point where they cross (color and other

the result, they would converge on the other side. A

aberrations are disregarded at this time). Such a lens

straight line drawn through the center of the two

may be thought of as consisting of an infinite number of

spherical surfaces is termed the axis of the lens. A

prisms arranged so that each directs light rays to the

central or axial ray would not be deviated because it

same single point. The lens bends the rays as a prism

would strike the surfaces of the lens at the normal. Such

does but, unlike a prism, it brings them to a point.

a ray would join the outer rays at their convergent point.

2-21